 |
AIfES 2
2.0.0
|
 |
AIfES 2
2.0.0
|
This tutorial shows based on an example, how to perform an inference in AIfES on an integer quantized Feed-Forward Neural Network (FNN). It is assumed, that the trained weights are already available or will be calculated with external tools on a PC. If you want to train the neural network with AIfES, switch to the training tutorial.
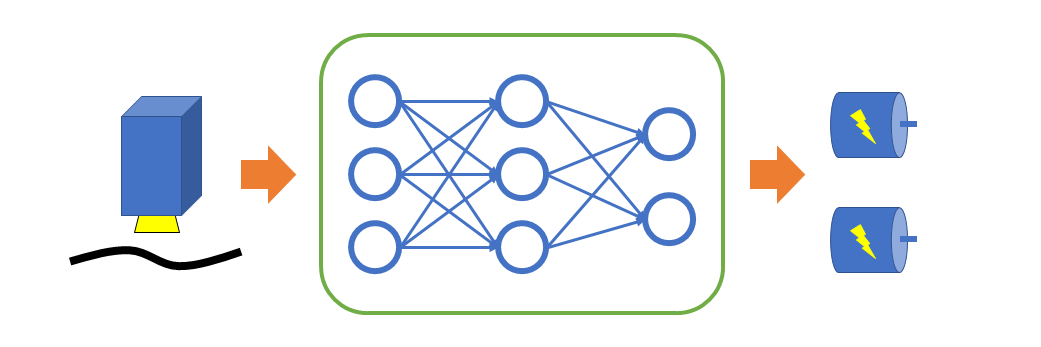
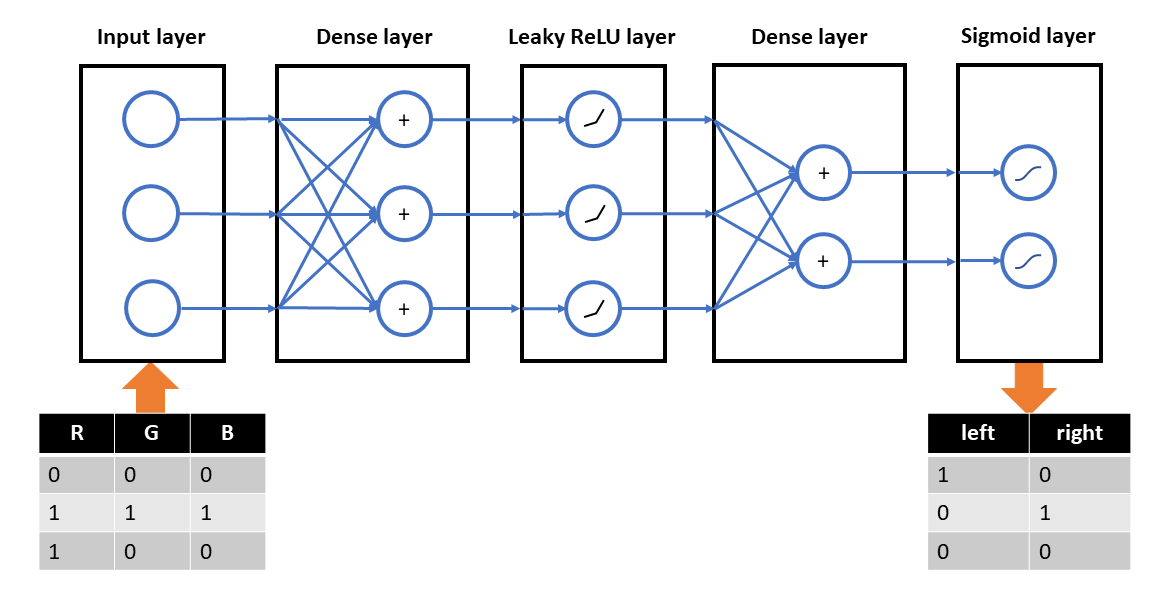
As an example, we take a robot with two powered wheels and a RGB color sensor that should follow a black line on a white paper. To fulfill the task, we map the color sensor values with an FNN directly to the control commands for the two wheel-motors of the robot. The inputs for the FNN are the RGB color values scaled to the interval [0, 1] and the outputs are either "on" (1) or "off" (0) to control the motors.

The following cases should be considered:
The resulting input data of the FNN is then
| R | G | B |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
and the output should be
| left motor | right motor |
|---|---|
| 1 | 0 |
| 0 | 1 |
| 0 | 0 |
To set up the FNN in AIfES 2, we need to design the structure of the neural network. It needs three inputs for the RGB color values and two outputs for the two motors. Because the task is rather easy, we use just one hidden layer with three neurons.
To create the network in AIfES, it must be divided into logical layers like the fully-connected (dense) layer and the activation functions. We choose a Leaky ReLU activation for the hidden layer and a Sigmoid activation for the output layer.
To perform an inference you need the trained weights and biases of the model. For example you can train your model with Keras or PyTorch, extract the weights and biases and copy them to your AIfES model.
For a dense layer, AIfES expects the weights as a matrix of shape [Inputs x Outputs] and the bias as a matrix of shape [1 x Outputs].
Example model in Keras:
Example model in PyTorch:
Our example weights and biases for the two dense layers after training are:
\[ w_1 = \left( \begin{array}{c} 3.64540 & -3.60981 & 1.57631 \\ -2.98952 & -1.91465 & 3.06150 \\ -2.76578 & -1.24335 & 0.71257 \end{array}\right) \]
\[ b_1 = \left( \begin{array}{c} 0.72655 & 2.67281 & -0.21291 \end{array}\right) \]
\[ w_2 = \left( \begin{array}{c} -1.09249 & -2.44526 \\ 3.23528 & -2.88023 \\ -2.51201 & 2.52683 \end{array}\right) \]
\[ b_2 = \left( \begin{array}{c} 0.14391 & -1.34459 \end{array}\right) \]
The Q7 quantization is an asymmetric 8 bit integer quantization that allows integer-only calculations on real values. The quantization procedure is closely related to the proposed techniques of the paper "Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference". A real value \( r \) is represented by an integer value \( q \), the scaling factor / shift \( s \) and the zero point \( z \) according to the following formula:
\[ r = 2^{-s} * (q - z) \]
To get the quantized value \( q \) out of a real value \( r \) you have to calculate
\[ q = round(\frac{r}{2^{-s}} + z) \]
To store the zero point and the scaling factor, a Q7 tensor needs additional parameters. These are stored in a structure of type aimath_q7_params_t and set to the tensor_params field of an aitensor_t. For example the tensor
\[ \left( \begin{array}{c} 0 & 1 & 2 \\ 3 & 4 & 5 \end{array}\right) \]
can be created with
or
Scalar values can be created with the structure aiscalar_q7_t and initialized either automatically with
or manually with
Also the macro functions FLOAT_TO_Q7(float_value, shift, zero_point) and Q7_TO_FLOAT(integer_value, shift, zero_point) are available for quick and easy conversion between float and integer values.
AIfES provides some helper functions to quantize 32 bit float values to 8 bit integer values. The following example shows how to automatically quantize a tensor with AIfES:
Asymmetric quantization (zero point != 0):
Symmetric quantization (zero point = 0):
To perform integer-only calculations, the first thing of an ANN we need to quantize are the intermediate results of the layers. Every layer needs to know in which range the values of its result are, in order to do the right calculations without any overflow. Therefor we have to perform some inferences on a representative part of the dataset (or the whole dataset) and remember the min and max values of each layers result tensor. Afterwards we can calculate the quantization parameters (shift and zero point) and configure them to the result tensors.
Example:
Our input dataset is given by the tensor
\[ \left( \begin{array}{rrr} 0 & 0 & 0 \\ 1 & 1 & 1 \\ 1 & 0 & 0 \end{array}\right) \]
The inference / forward pass for the layers gives us the following values:
Dense 1:
\[ \left( \begin{array}{rrr} 0.72655 & 2.67281 & -0.21291 \\ -1.38335 & -4.09500 & 5.13747 \\ 4.37195 & -0.93700 & 1.36340 \end{array}\right) \]
Leaky ReLU:
\[ \left( \begin{array}{rrr} 0.72655 & 2.67281 & -0.00213 \\ -0.01383 & -0.04095 & 5.13747 \\ 4.37195 & -0.00937 & 1.36340 \end{array}\right) \]
Dense 2:
\[ \left( \begin{array}{rrr} 8.00280 & -10.82488 \\ -12.87884 & 11.78870 \\ -8.08759 & -8.56308 \end{array}\right) \]
Sigmoid:
\[ \left( \begin{array}{rrr} 0.99967 & 0.00002 \\ 0.00000 & 0.99999 \\ 0.00031 & 0.00019 \end{array}\right) \]
Now we can calculate the quantization parameters (shift and zero point) with the value range (minimum and maximum values) of the result tensors of the input and dense layers. (The activation layers can calculate the quantization parameters on their own, because they just perform fixed transformations. Check the documentation to see if a layer needs manual calculation of the parameters or not.) For this we can use the aimath_q7_calc_q_params_from_f32() function. It is recommendet to add a small safety margin to the min and max values to deal with unseen data that results in slightly bigger values.
The min and max values and the resulting quantization parameters of the intermediate results of the layers are:
| layer | min | max | margin | shift | zero point |
|---|---|---|---|---|---|
| Input | 0 | 1 | 10 % | 7 | -70 |
| Dense 1 | -4.095 | 5.13747 | 10 % | 4 | -9 |
| Dense 2 | -12.878839 | 11.788695 | 10 % | 3 | 5 |
Example for quantization parameter calculation with margin:
In our simple example, we have two dense layers with weights and biases. For the integer model, we need to quantize the floating point values (given in the section above) to the integer type. To simplify the calculations of the inference, we use the symmetric quantization (zero point is zero). We perform a 8 bit integer quantization (Q7) on the weights and a 32 bit integer quantization (Q31) on the bias, to get an efficient tradeoff between performance, size and accuracy.
The maximum absolute value of the weight tensors and the resulting quantization parameters are
| tensor | max_abs | shift | zero point |
|---|---|---|---|
| Weights 1 | 3.6454 | 5 | 0 |
| Weights 2 | 3.23528 | 5 | 0 |
The shift of the (32 bit quantized) bias tensor is the sum of the related weights shift and result shift of the previous layer (This is due to the simple addition of the bias value to the internal accumulator without shift correction) are
| tensor | weights shift of same layer | result shift of previous layer | shift | zero point |
|---|---|---|---|---|
| Bias 1 | 5 | 7 | 12 | 0 |
| Bias 2 | 5 | 4 | 9 | 0 |
Tipp: Check the documentation of the layers in the Q7 datatype (e.g. of ailayer_sigmoid_q7_default()) to find the result shift of the activation layers. In addition, the function ailayer.calc_result_tensor_params can calculate the value.
The resulting integer values of the quantized weights and bias tensors are
\[ w_1 = \left( \begin{array}{c} 117 & -116 & 50 \\ -96 & -61 & 98 \\ -89 & -40 & 23 \end{array}\right) \]
\[ b_1 = \left( \begin{array}{c} 2976 & 10948 & -872 \end{array}\right) \]
\[ w_2 = \left( \begin{array}{c} -35 & -78 \\ 104 & -92 \\ -80 & 81 \end{array}\right) \]
\[ b_2 = \left( \begin{array}{c} 74 & -688 \end{array}\right) \]
AIfES provides implementations of the layers for different data types that can be optimized for several hardware platforms. An overview of the layers that are available for inference can be seen in the overview section of the main page. In the overview table you can click on the layer in the first column for a description on how the layer works. To see how to create the layer in code, choose one of the implementations for your used data type and click on the link.
In this tutorial we work with the int 8 data type (Q7 ) and use the default implementations (without any hardware specific optimizations) of the layers.
Used layer types:
Used implementations:
For every layer we need to create a variable of the specific layer type and configure it for our needs. See the documentation of the data type and hardware specific implementations (for example ailayer_dense_q7_default()) for code examples on how to configure the layers.
Our designed network can be declared with the following code.
We use the initializer macros with the "_M" (for "Manually") at the end, because we need to set our parameters (like the weights) to the layers.
If you already have the parameters of your model as a flat byte array (for example by quantization in python using the aifes-pytools or by loading the parameters from a stored buffer created with AIfES), you can use the automatic configuration of the layer. This way makes it easier to configure the neural network and to update new weight sets. On the other hand you lose some flexibility on where you store your data and it is harder to distinguish between the different values. Also the buffer format might change slightly with further updates of AIfES, so make shure that everything works out when updating.
We use the initializer macros with the "_A" (for "Automatically") at the end, because our parameters (like the weights) will be set by an aifes function to the layers.
Afterwards the layers are connected and initialized with the data type and hardware specific implementations
To see the structure of your created model, you can print a model summary to the console
Because AIfES doesn't allocate any memory on its own, you have to set the memory buffers for the inference manually. This memory is required for example for the intermediate results of the layers. Therefore you can choose fully flexible, where the buffer should be located in memory. To calculate the required amount of memory for the inference, the aialgo_sizeof_inference_memory() function can be used.
With aialgo_schedule_inference_memory() a memory block of the required size can be distributed and scheduled (memory regions might be shared over time) to the model.
A dynamic allocation of the memory using malloc could look like the following:
You could also pre-define a memory buffer if you know the size in advance, for example
To perform the inference, the input data must be packed in a tensor to be processed by AIfES. A tensor in AIfES is just a N-dimensional array that is used to hold the data values in a structured way. To do this in the example, create a 2D tensor of the used data type. The shape describes the size of the dimensions of the tensor. The first dimension (the rows) is the batch dimension, i.e. the dimension of the different input samples. If you process just one sample at a time, this dimension is 1. The second dimension equals the inputs of the neural network.
You can also create a float 32 tensor and let it quantize by AIfES:
Now everything is ready to perform the actual inference. For this you can use the function aialgo_inference_model().
Alternative you can also do the inference without creating an empty tensor for the result with the function aialgo_forward_model(). The results of this function are stored in the inference memory. If you want to perform another inference or delete the inference memory, you have to save the results first to another tensor / array. Otherwise you will loose the data.
Afterwards you can print the results to the console for debugging purposes:
If you want to get F32 values out of the Q7 tensor, you can use the macro Q7_TO_FLOAT(integer_value, shift, zero_point) as explained earlier:
If you have a trained F32 model in AIfES and you want to convert it to a Q7 quantized model (for example to save memory needed for the weights or to speed up the inference), you can use the provided helper function aialgo_quantize_model_f32_to_q7(). To use this function, you need to have the F32 model and a Q7 model skeleton with the same structure as the F32 model. Also a dataset is needed that is representative for the input data of the model (for example a fraction or all of the training dataset) to calculate the quantization range.
Example:
If you have the example model, described in the F32 training tutorial or the F32 inference tutorial , you have to build up a Q7 model skeleton that looks like this:
In Addition you need to set the parameter memory and the inference memory to the model. In the parameter memory, the quantized parameters (weights, biases, quantization parameters) will be stored and the inference memory is needed to perform the quantization.
Then you need the mentioned representative dataset of the input data. In this case we simply take the training dataset because it is very small and has no representative subset.
Now you can perform the quantization by calling aialgo_quantize_model_f32_to_q7().
The Q7 model is now ready to use for example to run an inference. You can also store the parameter memory buffer in your storage memory after the model is quantized and later on load it using the layer declaration described above.
To automatically quantize a model using python (for example a Keras or PyTorch model) you can use our AIfES Python tools. You can install the tools via pip with:
pip install https://github.com/Fraunhofer-IMS/AIfES_for_Arduino/raw/main/etc/python/aifes_tools.zip
The the quantized model can either be setup manually with the calculated weights and quantization parameters (result_q_params, weights_q_params and weights_q7) or setup automatically by using the buffer printed by the print_flatbuffer_c_style() function.
Example: Quantize a tf.keras model:
Example: Quantize a PyTorch model